The sliding window technique is a popular algorithmic method used to solve a variety of problems efficiently, particularly those that involve arrays or lists. The core idea is to maintain a subset of elements within a larger collection and “slide” through the data to find solutions without needing to repeatedly reprocess the entire set. This approach is both time-efficient and elegant, making it a go-to method for many coding challenges.
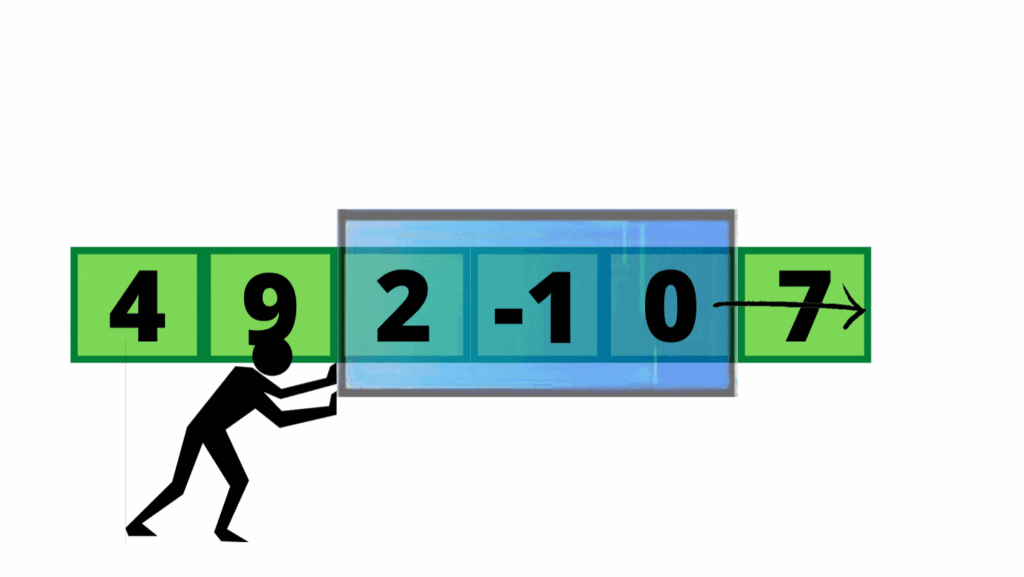
How It Works
Imagine you have a window that can cover a certain portion of an array. This window can move from left to right across the array, one element at a time. As it moves, you update the contents of the window based on the current position, and the window size can either be fixed or variable depending on the problem.
Types of Sliding Window Problems
- Fixed-Size Sliding Window:
- Example Problem: Find the maximum sum of a subarray with a fixed length.
- How It Works: Start by calculating the sum of the first window of elements. Then, for each subsequent position, subtract the element that is leaving the window and add the element that is entering the window. This way, you avoid recalculating the sum from scratch for each position.
- Variable-Size Sliding Window:
- Example Problem: Find the smallest subarray with a sum greater than a given value.
- How It Works: Start with an empty window, then expand it by adding elements until the sum exceeds the target. Once it does, shrink the window from the left to try and find the smallest possible subarray that meets the criteria.
Why Use the Sliding Window Technique?
- Efficiency: It reduces the time complexity of problems that would otherwise require nested loops, often bringing down a solution from O(n^2) to O(n).
- Simplicity: The logic is straightforward and easy to implement once understood.
- Applicability: It can be used in a wide range of problems, such as finding maximums, minimums, or specific conditions within subarrays.
Example Code: Maximum Sum of a Subarray (Fixed Window)
Here’s a simple Python implementation of the sliding window technique to find the maximum sum of a subarray with a fixed size.
def max_sum_subarray(arr, k):
n = len(arr)
max_sum = sum(arr[:k])
window_sum = max_sum
for i in range(n - k):
window_sum = window_sum - arr[i] + arr[i + k]
max_sum = max(max_sum, window_sum)
return max_sum
# Example usage
arr = [2, 1, 5, 1, 3, 2]
k = 3
print(max_sum_subarray(arr, k)) # Output: 9
Conclusion
The sliding window technique is a powerful and versatile tool in your algorithmic toolkit. By mastering it, you can tackle a wide range of problems more efficiently. Start with simple fixed-size window problems to get comfortable with the concept, then move on to more complex scenarios involving variable window sizes. Happy coding!